En 2001-2002, alors que je n’étais pas encore titulaire, j’avais à encadrer des travaux pratiques d’informatique en 2e année de Licence de chimie à l’université. Ceux-ci devaient être réalisés en Visual Basic (un choix indépendant de ma volonté). Afin d’entraîner les étudiants à manipuler des variables, des tableaux, des boucles et des structures décisionnelles, je leur avais proposé de programmer un « Jeu de la vie ». L’intérêt est, qu’en plus, ils pouvaient dessiner une interface graphique agréable (boutons, menus déroulants, courbes, image…) et réellement s’amuser avec leur jeu de la vie, une fois au point. Comme je trouve dommage que mon travail soit resté dans un carton, je donne ci-après le document que j’avais rédigé et les directives pour ce projet informatique.
Projet informatique en Visual Basic : Jeu de la vie
Proposé par C. Darrigan
Introduction
Inventé par le mathématicien John Horton Conway au début des années 1970, le « jeu de la vie » (Game Life ou Life en anglais) se présente sous la forme d’un quadrillage, plus ou moins grand, dont l’état de chaque case (noir ou blanc) à un instant n est déterminé par des règles de base très simples et par l’état des cases qui l’entourent, à l’instant n – 1. Le « jeu de la vie » fait partie de la famille plus générale des automates cellulaires, eux-mêmes entrant dans la catégorie des simulations de type Monte Carlo (en référence à la ville célèbre pour ses jeux de hasard) dans lesquelles l’évolution d’un système (plus complexe que de simples cases noires ou blanches) dépend de quelques règles simples d’évolution ou d’interactions. De très nombreux domaines scientifiques utilisent ce type de modélisation en raison de la grande facilité de réalisation informatique (programmation) et de l’impressionnante concordance des simulations avec les observations expérimentales. On citera quelques domaines et applications :
- Physique : simulation d’écoulements, transfert de chaleur, résistance des matériaux, météorologie…
- Chimie : optimisation géométrique de molécules complexes, mécanique moléculaire, dynamique moléculaire, diffusion de molécules dans des solides poreux, simulation de polymères, transitions de phase…
- Biologie : modélisation de grosses molécules (ADN, protéines, etc), de leur configuration spatiale, de leurs interactions, simulation de comportements collectifs (fourmis, bactéries, etc)…
- Informatique : réseaux de neurones, automates cellulaires, vie et intelligence artificielles…
- Mathématiques : logique, indécidabilité, phénomènes chaotiques…
Vocabulaire et quelques propriétés
- On appellera monde ou quadrillage ou tableau l’espace dans lequel le jeu se déroule. Il s’agit en général d’un espace borné.
- On appelle cellule ou case ou pixel l’unité de base du quadrillage, pouvant prendre deux valeurs : 0 ou 1.
- On définit la population comme le nombre de cases de valeur 1.
- Un système est divergent s’il conduit à un monde totalement remplis de 0 ou de 1.
- Un système est convergent si sa population tend vers ou fluctue autour d’une valeur.
- Un système est cyclique d’ordre m si sa population totale fluctue régulièrement, avec une période de m itérations.
- Certains systèmes sont pseudo-cycliques avec soit une convergence, soit une divergence au bout d’un temps long.
- Un appelle motif un groupe de cases (l’exemple ci-dessous montre l’évolution d’un motif)
- Certains motifs peuvent se déplacer d’eux-même dans le monde en gardant la même structure, on les appelle des planeurs.
- Certains motifs augmentent en taille indéfiniment, on les appelle des remplisseurs.
- Les remplisseurs qui ont la propriété de « manger » les autres motifs sont appelés démons.
- Une configuration est appelé Jardin d’Eden si elle n’est le résultat d’aucune configuration par les règles établies.
- On appellera soupe un monde généré aléatoirement.
- Le comportement à long terme d’un jeu de la vie est indécidable : cela signifie qu’aucune démonstration ni aucun algorithme ne permet de prédire le devenir d’un système à long terme.
- Le jeu de la vie est déterministe : cela signifie que les mêmes conditions initiales conduisent aux mêmes configurations quelle que soit l’itération.
- Lorsqu’il est généré à partir d’une soupe, il est souvent chaotique : aucune régularité n’apparaît au cours des itérations. Une légère modification des conditions initiales peut conduire à un résultat totalement différent.
- Un système est irréversible si, étant donné une configuration, il est impossible de déterminer la configuration de l’itération précédente de manière unique. Le jeu de la vie possède généralement cette propriété.
Exemples
Si nous prenons comme règle de base qu’une cellule ne peut survivre que lorsqu’elle est entourée de 2 ou 3 cellules, voici les 9 premières itérations d’évolution d’un motif primitif :
On peut remarquer qu’après un temps de croissance, le système devient cyclique d’ordre 2 à partir de l’itération 6. Il est donc convergent. On remarque aussi que le motif ne semble pas se déplacer dans une direction particulière au fil des itérations. Voici quelques itérations d’un système stable de dimension 30×30 à partir d’une soupe. Le système converge rapidement, la population fluctue autour d’une valeur.
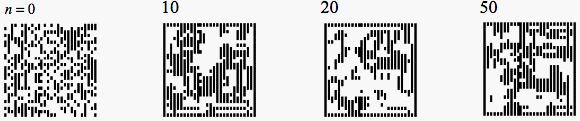
Evolution d’une soupe après 10, 20 et 50 itérations.
La figure ci-après apparaîtra-t-elle un jour, ou non ?… si elle apparaît, il ne faut surtout pas l’interpréter comme un signe paranormal !

Jardin d’Eden ?
Votre projet
Ce genre de jeu de la vie est très intéressant à programmer car il fait appel aux principales structures de bases : boucles imbriquées, tests conditionnels, manipulation de tableaux, affichage sous forme graphique… La réalisation du projet, si elle est menée jusqu’au bout (et sans « recopiage » de la part des étudiants !), est une preuve de la bonne compréhension de l’outil informatique. Elle fait aussi appel au grand potentiel créatif de l’étudiant, tant au niveau de l’algorithme (car il n’y a pas qu’une seule méthode possible pour fabriquer ce jeu), qu’au niveau de la programmation et de la présentation graphique du logiciel. Le Visual Basic est un outil bien adapté à la réalisation d’applications très soignées.
Votre projet consiste donc à simuler l’évolution d’une population de bactéries, en laissant à l’utilisateur la possibilité de choisir lui-même :
- La dimension du monde dans lequel va se dérouler le jeu
- La densité des bactéries à l’état initial
- Les règles de vie et de mort
- Le passage à l’itération suivante
Le monde sera modélisé par un tableau rectangulaire de dimensions dimi sur dimj, dans lequel les cases auront soit la valeur 0 (cellule vide, pas de bactérie) soit la valeur 1 (cellule occupée par une bactérie). La valeur d’une case devra changer au fil des itérations en fonction de l’état de ses premières voisines et des règles de vie et de mort. Ce travail peut donc se découper en deux parties distinctes :
- Génération de la soupe primitive
Il s’agit de créer le monde de l’instant initial n = 0, en y répartissant de manière aléatoire les bactéries. L’utilisateur devra pouvoir choisir la densité initiale en bactéries, comprise entre 0% pour un monde sans bactérie (toutes les cases à 0) et 100% pour un monde totalement peuplé (toutes les cases à 1).
- Évolution du monde
Le monde devra évoluer en fonction des règles de vie et de mort choisies par l’utilisateur en cliquant sur un bouton. Les règles peuvent être résumées comme suit :
- Règle de vie : une case vide entourée d’au moins V bactéries contiendra une bactérie à l’itération suivante
- Règle de mort : une bactérie entourée d’au moins M bactéries mourra d’étouffement à l’itération suivante (avec M > V)
- Dans les autres cas, la case reste inchangée, qu’elle soit occupée ou non.
(On prendra par exemple V=2 et M=4.) Une étape indépendante, pouvant faire l’objet d’une subroutine, consistera à donner une image graphique (cases noires et blanches) du tableau dans un objet PictureBox. Un tel jeu est très amusant à essayer tant les observations que l’on peut en tirer sont nombreuses et captivantes. Il permet de montrer que des règles de base très simples peuvent suffire à engendrer des phénomènes très riches et diversifiés de la vie, sans prétendre décrire tout de la vie, bien sûr ! Nous espérons que vous « accrocherez » à ce projet et que vous y prendrez goût autant que nous avons pris plaisir à vous le préparer !
Améliorations possibles…
Une fois le jeu de la vie programmé, vous pouvez améliorer et étoffer votre projet à l’aide des options ci-dessous (classées par ordre de difficulté croissante) :
- Afficher la population à chaque itération (cette option est très utile).
- Tracer une courbe de population en fonction des itérations (cette option est très pratique pour visualiser la stabilité d’un monde, ses divergences, son caractère cyclique).
- Possibilité de sauvegarder une image du monde sur fichier et de pouvoir la relire plus tard.
- Possibilité d’ajouter ou de supprimer manuellement des bactéries en cliquant dans l’image.
- Modéliser un espace torique, dans lequel le tableau est bouclé en faisant correspondre le haut avec le bas et la gauche avec la droite (pour les plus doués d’entre vous !).
Ou, selon votre inspiration, tout un tas d’autres options que vous souhaiterez utiles à la compréhension ou la manipulation du jeu.
Évaluation de votre projet
Vous serez notés essentiellement sur votre capacité à transformer un problème donné en un algorithme informatique. Si vous n’arrivez pas à terminer votre programme, ce n’est pas grave. Par contre, essayez de faire un code propre et lisible (indentation, noms de variables explicites), contenant si possible quelques commentaires. Attachez une certaine part d’importance à l’aspect graphique de votre application (dimensions et dispositions des boutons, des cases à remplir, couleurs). Pour les meilleurs, les améliorations ci-dessus seront bienvenues !
Petite aide…
Vous pouvez obtenir de l’aide à partir du menu déroulant « ? » de Visual Basic. Voici quelques fonctions dont vous aurez peut-être besoin :
- Instruction Randomize : elle permet d’initialiser le générateur de nombre aléatoire du programme, en l’insérant en tête de votre code.
- Fonction Rnd() : elle retourne un nombre aléatoire compris entre 0 (inclus) et 1 (exclus).
- Structure Select case : permet de réaliser différentes alternatives en fonction d’une variable. Dans certains cas, elle peut être plus facile à utiliser qu’une structure If then else.
- Tableau à 2 dimensions : vous en aurez besoin pour décrire le monde.
Exemple : M(3,2)=1 donne la valeur 1 à la case repérée par la ligne 3 et la colonne 2
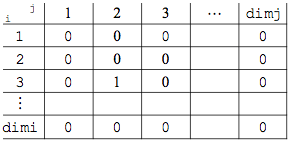
Tableau à 2 dimensions.
Ne pas confondre les indices avec la valeur contenue dans une case. Pour passer en revue chacune des cases, on utilisera une boucle FOR NEXT sur les colonnes à l’intérieur d’une boucle FOR NEXT sur les lignes.
Pour ceux qui veulent juste s’amuser avec un jeu de la vie, et non pas le programmer, voir ce bon site.
Voir aussi : Le hasard a besoin de temps pour créer de belles choses
Voir aussi la page Wikipédia : Jeu de la vie

