avec n = 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16

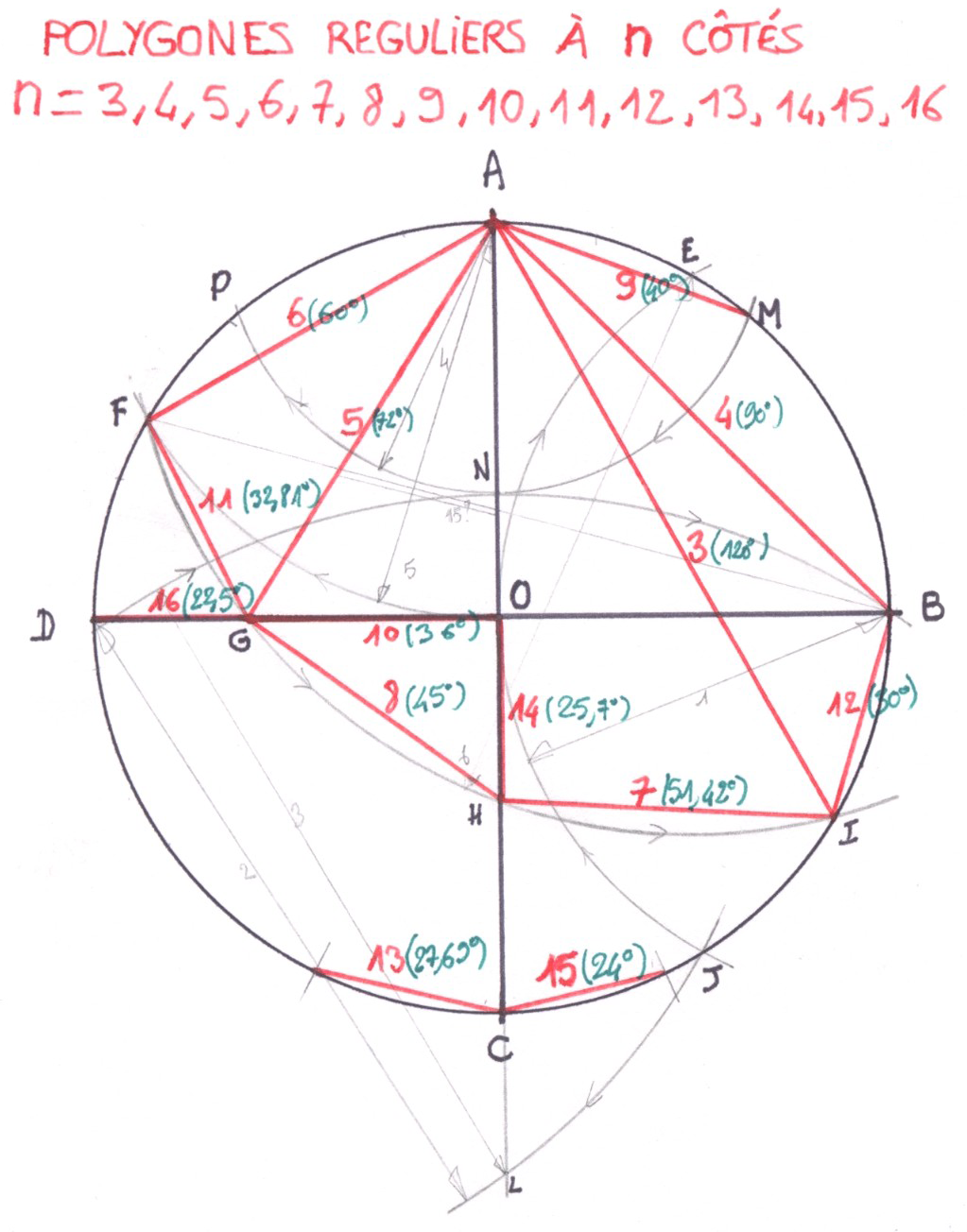
Constructions à la règle et au compas pour trouver les longueurs des côtés de polygones à n côtés (n indiqué en rouge).

Permet aussi de diviser une tarte en 3, 4, 5, …, 16 parts égales (angle indiqué en vert) chez des amis, tout en passant pour un extraterrestre.

• Tracer un segment [AC], trouver sa médiatrice au compas et la tracer, elle coupe [AC] en O. Pointe en O, tracer le cercle passant par A, il coupe la médiatrice en B et D.
• [AB] = P(4) (comprendre : le segment AB est le côté du polygone régulier à 4 côtés).
• Pointe en B, tracer l’arc n°1 (indiqué au crayon) passant par O. Celui-ci coupe le cercle en J et E.
• Pointe en D, tracer l’arc n°2 partant de J, coupant (AC) en L.
• Pointe en L, tracer l’arc n°3 partant de D, coupant [OA] en N et rejoignant B.
• Pointe en A, tracer l’arc n°4 partant de N, coupant le cercle en M et P.
• [AM] = P(9)
• Pointe en A, tracer l’arc n°5 partant de O, coupant le cercle en F.
• [AF] = P(6)
• Pointe en E, tracer l’arc n°6 partant de F, coupant [OD] en G et [OC] en H, et le cercle en I.
• [FG] = P(11), [GH] = P(8), [HI] = P(7), [BI] = P(12), [OG] = P(10), [DG] = P(16), [OH] = P(14), [AI] = P(3)
• Compas de rayon [OG], pointe en I, tracer l’arc coupant le cercle en K (non indiqué sur la figure, à côté de J).
• [CK] = P(15)
• Pour P(13), j’ai perdu la trace…

Source : l’excellent livre Créer avec un compas, Daniel-Jacques Allonsius, éditions Dessain et Tolra (1986).